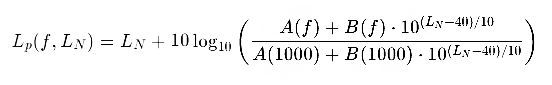Las curvas isofónicas, también conocidas como curvas de igual sonoridad, representan el nivel de presión sonora (SPL, por sus siglas en inglés) necesario para que una persona perciba un sonido de una frecuencia determinada con la misma sensación de volumen que un tono de referencia. Estas curvas se expresan en fonios (phons), una unidad de medida que relaciona la intensidad subjetiva del sonido con el nivel de presión sonora en decibelios (dB SPL).

El oído humano no responde de manera uniforme a todas las frecuencias. En general, somos más sensibles a las frecuencias entre 2 kHz y 5 kHz, donde el sistema auditivo es más eficiente. En cambio, los sonidos de baja frecuencia requieren niveles de presión sonora significativamente más altos para ser percibidos con la misma intensidad.

Historia y Desarrollo

Las primeras curvas isofónicas fueron desarrolladas en la década de 1930 por los investigadores Harvey Fletcher y Wilden A. Munson en los laboratorios Bell, basándose en estudios de percepción auditiva. A lo largo del tiempo, estas curvas han sido refinadas, destacando los estudios de Robinson y Dadson en 1956 y la estandarización actual bajo la norma ISO 226:2003.

Modelado Matemático de las Curvas Isofónicas

El modelo actual de las curvas isofónicas se define mediante la ecuación estándar de la norma ISO 226:2003:

donde:

Lp (f,Ln) es el nivel de presión sonora en dB SPL para la frecuencia f y la curva de sonoridad Ln en fonios.
A (f) y B  (f)  son funciones empíricas que dependen de la frecuencia y han sido definidas experimentalmente.
Ln es el nivel de sonoridad en fonios.

Interpretación de las Curvas Isofónicas

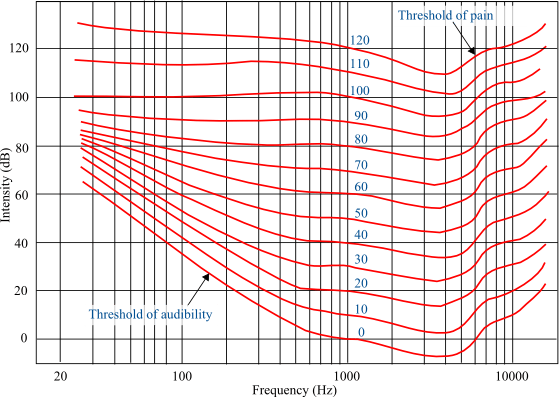
Cada curva isofónica muestra los niveles de presión sonora requeridos para que diferentes frecuencias sean percibidas con la misma intensidad subjetiva. Algunos puntos clave de interpretación incluyen:

A 1 kHz, el valor en fonios es equivalente al nivel de presión sonora en dB SPL (por ejemplo, 60 fonios corresponden a 60 dB SPL a 1 kHz).
En frecuencias bajas (<100 Hz), la sensibilidad auditiva es menor, por lo que se requieren mayores niveles de SPL.
En frecuencias altas (>10 kHz), también se observa una disminución de la sensibilidad, aunque en menor medida que en bajas frecuencias.

Aplicaciones en Acústica y Sonido Profesional

El conocimiento de las curvas isofónicas es crucial en diversas áreas del sonido profesional, incluyendo:

Diseño de altavoces y sistemas de refuerzo sonoro: Para optimizar la respuesta en frecuencia de un sistema de sonido y garantizar una percepción equilibrada en todo el espectro audible.
Masterización y mezcla de audio: Los ingenieros de sonido utilizan las curvas isofónicas para ajustar la ecualización de manera que el contenido sonoro tenga un balance adecuado en distintas condiciones de escucha.
Normativas de ruido y salud auditiva: La evaluación del impacto del ruido en el bienestar humano se basa en la percepción real de la intensidad del sonido, lo que permite establecer límites adecuados de exposición.

Gráfico de Curvas Isofónicas

Conclusión

Las curvas isofónicas son fundamentales para comprender la percepción del sonido y optimizar la reproducción auditiva en diferentes contextos. Desde la ingeniería de sonido hasta la psicoacústica, estas curvas proporcionan información esencial para el desarrollo de tecnologías y entornos sonoros que se alineen con la sensibilidad del oído humano.