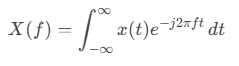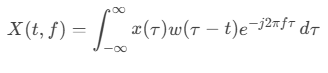Fondements Mathématiques : De la Transformée de Fourier à la STFT

 

Transformée de Fourier Continue (TF)

 

La Transformée de Fourier (TF) d’un signal continu x(t)x(t)x(t) est définie comme :

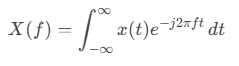
Cette représentation indique quelles fréquences sont présentes dans le signal, mais ne montre pas quand elles apparaissent. Pour les signaux stationnaires (dont les propriétés ne changent pas dans le temps), la TF est suffisante. Cependant, l’audio est un signal non stationnaire, nécessitant une approche différente.

 

Transformée de Fourier à Court Terme (STFT)

 

La STFT introduit une fenêtre glissante w(t)w(t)w(t) qui isole de courts segments du signal avant d’appliquer la TF. Mathématiquement :

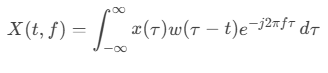
Où :

w(t)w(t)w(t) est une fonction fenêtre (par ex. Hann, Hamming, Blackman).
ttt est l’instant temporel analysé.
fff est la fréquence.
La STFT produit une représentation temps-fréquence, qui peut être visualisée à l’aide d’un spectrogramme.

---

 

Paramètres Clés de la STFT

 

La qualité et la résolution de la STFT dépendent de :

Taille de la fenêtre (N) :

Fenêtres plus grandes → meilleure résolution en fréquence, mais résolution temporelle plus faible.
Fenêtres plus petites → meilleure résolution temporelle, mais résolution en fréquence plus faible (Principe d’incertitude de Heisenberg-Gabor).
Recouvrement (Overlap) :

Pour éviter la perte d’informations, un recouvrement de 50 % à 75 % est généralement utilisé.
Type de fenêtre :

Rectangulaire : simple mais avec des lobes secondaires élevés (fuites spectrales).
Hann/Hamming : réduit les fuites spectrales, mieux adapté à l’analyse spectrale.

 

Spectrogramme : Visualisation du domaine temps-fréquence

 

Un spectrogramme est une représentation graphique de la magnitude de la STFT (∣X(t,f)∣) :

Axe X : Temps
Axe Y : Fréquence
Couleur/Intensité : Énergie (dB) ou amplitude
Exemples de caractéristiques observables dans un spectrogramme audio :

Formants : bandes d’énergie élevée correspondant aux résonances du conduit vocal.
Harmoniques : composantes périodiques des signaux d’instruments de musique. 

Types de spectrogrammes

 

• Spectrogrammes spécialisés

  Spectrogramme d’amplitude

  Affiche ∣X(t,f)∣|X(t,f)|∣X(t,f)∣.
  Montre directement la magnitude du signal à chaque instant et fréquence.
  Spectrogramme de puissance

  Affiche ∣X(t,f)∣2|X(t,f)|^2∣X(t,f)∣2.
  Représente l’énergie du signal, utile pour analyser l’intensité relative des composants fréquentiels.
  Spectrogramme à échelle logarithmique

  Fréquences affichées sur une échelle logarithmique (ex. échelle Mel).
  Correspond mieux à la perception humaine du son, pratique pour la musique et la voix.

   

---

 

Applications de l’analyse temps-fréquence en audio

 

Compression Audio (par ex., MP3, AAC)

 

• La STFT identifie les composantes non pertinentes (masquage auditif) pour une compression sélective

 

Reconnaissance de la parole et de la musique

 

• Extraction des MFCC (coefficients cepstraux en fréquence de Mel), basés sur des banques de filtres appliquées au spectrogramme.

 

Synthèse et modification audio

 

• Étirement temporel et modification de la hauteur (ex. : Phase Vocoder).
  Réduction du bruit : filtrage temps-fréquence (ex. : Filtrage de Wiener).

 

Analyse des instruments de musique

 

• Identification des harmoniques partielles et des transitoires.

---

 

Limitations et alternatives

 

Limitations de la STFT

 

• Compromis temps-fréquence : impossible d’obtenir une haute résolution simultanément dans les deux domaines.
• Effet de flou : dû à la convolution avec la fenêtre.

 

Méthodes alternatives

 

• Transformée en ondelettes : meilleure résolution temporelle pour les hautes fréquences.
• Analyse des composants spectraux (PCA/ICA) : pour les signaux complexes.
• Distribution de Wigner-Ville : précision plus élevée, mais avec interférences entre termes croisés.

---

 

Conclusions

 

 

L’analyse de Fourier dans le domaine temps-fréquence (STFT + spectrogramme) est une technique puissante pour le traitement audio, permettant :

La visualisation de l’évolution des fréquences.
L’extraction de caractéristiques pour l’apprentissage automatique.
La modification et la synthèse sonore.
Cependant, son efficacité dépend d’un choix approprié des paramètres (type de fenêtre, recouvrement, taille de la FFT). Pour des applications avancées, des méthodes comme les ondelettes ou les modèles basés sur des réseaux neuronaux (par ex. TF-GAN, Wavenet) peuvent être explorées.

References

• Oppenheim, A. V., & Schafer, R. W. (2010). Discrete-Time Signal Processing.
• Smith, J. O. (2007). Spectral Audio Signal Processing.
• Mallat, S. (2008). A Wavelet Tour of Signal Processing.