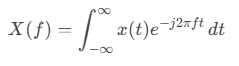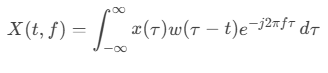Explore o Mundo do Áudio Profissional
Análise de Fourier Aplicada ao Áudio: Domínio Tempo-Frequência
A análise de Fourier é uma ferramenta matemática fundamental no processamento de sinais, permitindo a decomposição de um sinal no domínio do tempo em seus componentes de frequência. No contexto do áudio, essa análise é essencial para tarefas como compressão, filtragem, síntese e reconhecimento de padrões.
No entanto, como os sinais de áudio são dinâmicos e variam ao longo do tempo, a análise de Fourier clássica (baseada na Transformada de Fourier) é insuficiente, pois fornece apenas informação no domínio da frequência sem considerar a evolução temporal.
Para resolver esse problema, utilizam-se técnicas de análise tempo-frequência, que permitem estudar como o conteúdo espectral de um sinal de áudio muda ao longo do tempo. Entre essas técnicas, destacam-se:
-
Transformada de Fourier de Curto Prazo (STFT)
-
Transformada Wavelet (WT)
-
Distribuições de Energia Tempo-Frequência (por exemplo, Espectrograma, Wigner-Ville)
Este documento explora a análise de Fourier aplicada ao áudio em detalhe, com foco na STFT e na sua representação por meio de espectrogramas.
Análise Tempo-Frequência de Áudio: STFT, Espectrogramas e Aplicações da Fourier
Artigos em Destaque
Tecnare
Séries de Alto-falantes
E Series
IBZA Series
V Series
ALIS Series
Array Series
SW Series
KT Series
TANIT Series
CS Series
Amplifiers Series
Digital Processors
Accessories
IK Series
PS Series
LTS Series